Pochodne funkcji
Tworzenie pochodnej
Aby utworzyć pochodną funkcji należy korzystać ze wzorów, które są podane w tablicach matematycznych (warto jednak zapamiętać je, aby szybciej wykonywać takie zadania)

Tablice matematyczne podają kilka kolejnych wzorów, lecz najważniejsze są te, które widać powyżej.
Tutaj możemy zauważyć, że pierwsze cztery wzory to jeden i ten sam wzór. Wzór ten polega na tym, że mamy daną liczbę axb, aby zrobić z niej pochodną należy ją przekształcić na następującą liczbę: baxb-1
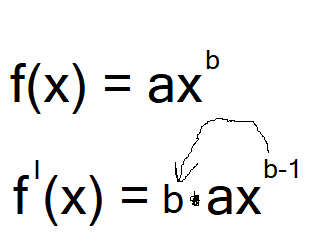
Teraz sprawdźmy, czy to prawda, że pierwsze cztery przykłady z tabeli podlegają pod ten sam wzór.
Przykład 1
$$f(x)=c$$
Tutaj za c możemy podstawić x0, ponieważ wszystko do potęgi 0 jest równe 1, a gdy pomnożymy c przez 1 dalej wychodzi c, więc nie zmieniamy równania.
$$f(x)=cx^0$$
Teraz podstawiamy pod nasz wzór
$$f^\prime(x)=0\times cx^{0-1}$$
$$f^\prime(x)=0\times cx^{-1}$$
$$f^\prime(x)=0$$
Przykład 2
$$f(x)=ax$$
Tu można od razu podstawić do wzoru (należy pamiętać, że samo x bez potęgi to inaczej x1)
$$f^\prime(x)=1\times ax^{1-1}$$
$$f^\prime(x)=ax^0$$
$$f^\prime(x)=a$$
Przykład 3
$$f(x)=ax^2 + bx + c$$
$$f^\prime(x)=2\times ax^{2-1}+1\times bx^{1-1} + 0\times cx^{0-1}$$
$$f^\prime(x)=2ax+b$$
Przykład 4
Tutaj możemy zauważyć, że to jest wzór, który testujemy na tych przykładach, ale bez liczby przed x, ale możemy podstawić, aby sprawdzić, czy na pewno wyjdzie.
$$f(x)=x^r$$
$$f^\prime(x)=rx^{r-1}$$
Oczywiście licząc pochodne nie musimy podstawiać idealnie do wzoru, robię to tylko w celach szczegółowej prezentacji, jak to wygląda, normalnie najlepiej funkcję f(x) = ax2 + bx + c od razu zapisać w postaci pochodnej f'(x) = 2ax + b
Kolejne dwa wzory podane w tabelce najlepiej zapamiętać. Jedną z ważniejszych czynności jest obliczenie dziedziny jeszcze przed jakimkolwiek przekształcaniem równania. Jest to ważne, poniższy przykład idealnie to prezentuje:
Przykład 5
Określ, czy dwie podane funkcje są te same?
$$f(x)=x$$$$g(x)={x^2 \over x}$$
Odpowiedź:
Funkcje nie są te same.
Wyjaśnienie:
Pierwsza funkcja (f(x)) jest zwykłą linią, której dziedziną jest zbiór liczb rzeczywistych (R), druga zaś (g(x)) to taka sama linia, lecz będzie ona przerywana w punkcie x=0, bo nie można dzielić przez 0, dlatego właśnie ma inną dziedzinę i będzie miała dziurę w punkcie x=0, przec co jest to inna funkcja.
W tablicach znajdują się też wskazówki co robić, gdy funkcja składa się z kilku części (np.: 2x+5x2 lub 5x * 12x2)
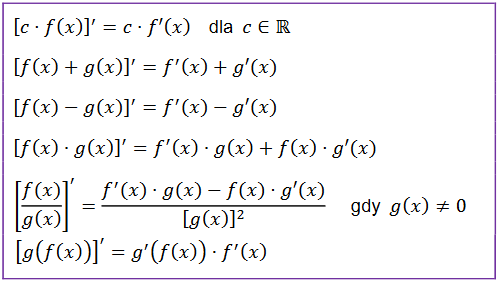
Trzy ostatnie wzory są już bardziej rozbudowane, ostatni dotyczy funkcji złożonych, które będziemy przerabiać w następnym temacie, więc teraz będziemy przerabiać dwa pozostałe spośród trudniejszych
Wzór 1
Wzór ten pokazuje, że jeśli mnożymy liczbę stałą (czyli bez zmiennej) przez zmienną, to liczymy pochodną tylko ze zmiennej, a stałą zostawiamy. Przykład:
$$f(x)=8x^2$$
W tym przykładzie tak naprawdę ignorujemy na początek liczbę 8 która jest stała i liczymy pochodną z x^2.
$$f^\prime(x)=8 \times 2x$$
Dopiero na końcu mnożymy przez pozostałą stałą, czyli 8.
$$f^\prime(x)=16x$$
Wzór 2 i Wzór 3
Te dwa wzory pokazują, że dodawanie i odejmowanie dotyczą osobnych części, czyli w przypadku funkcji f(x) = 3x2 + 2x - 10 Mamy trzy różne części i każdą z nich traktujemy osobno i liczymy pochodne osobno, przez co wychodzi f(x) = 6x + 2
Wzór 4 i Wzór 5
Te dwa wzory trzeba znać, są one bardzo ważne. Prawdą jest, że czasami można policzyć takie pochodne po prostu obliczając działania na początku i wykorzystując prostszych wzorów, ale czasem nie będzie to możliwe.
Zadanie 1
Oblicz pochodną funkcji.
| a) | $$f(x)=2x^3+3x-\sqrt{x}+{5\over x} + {\sqrt[4]{52}\times \sqrt[4]{31}+57\pi \over 91\pi - \sqrt[3]{1092}}$$ | $$f^\prime(x)=6x^2+3 - {1\over 2\sqrt{x}} - {5 \over x^2}$$Wyjaśnienie: W tym zadaniu najzwyczajniej podstawiamy do wzorów i wychodzi wynik. Gigantyczny ułamek może przerazić, ale to tylko stała, więc po obliczeniu na pochodną cały ułamek będzie równy 0 | |
| b) | $$f(x)=(2x^3+2x)(3x^2-4x^4)$$ | $$f^\prime(x)=-56x^6-10x^4+18x^2$$ Wyjaśnienie: To zadanie można rozwiązać na dwa sposoby, można pomnożyć dwa nawiasy i z wyniku policzyć pochodną lub skorzystać z wzoru. Ja skorzystam z wzoru aby go utrwalić.$$f^\prime(x)=(2x^3+2x)^\prime(3x^2-4x^4) + (2x^3+2x)(3x^2-4x^4)^\prime$$$$f^\prime(x)=(6x^2+2)(3x^2-4x^4)+(2x^3+2x)(6x-16x^3)$$$$f^\prime(x)=18x^4-24x^6+6x^2-8x^4+12x^4-32x^6+12x^2-32x^4$$$$f^\prime(x)=-56x^6-10x^4+18x^2$$ | |
| c) | $$f(x)={2x+5\over x^2-2}$$ | $$f^\prime(x)=$$ Wyjaśnienie: Tutaj skorzystałem ze wzoru (UWAGA: dół ułamka najlepiej zostawić i nie obliczać potęgi, pomoże to przy obliczaniu dziedziny):$$f^\prime(x)={(2x+5)^\prime(x^2-2)-(2x+5)(x^2-2)^\prime \over (x^2-2)^2}$$$$f^\prime(x)={2(x^2-2)-(2x+5)2x \over (x^2-2)^2}$$$$f^\prime(x)={2x^2-4-4x^2+10x \over (x^2-2)^2}$$$$f^\prime(x)={6x^2+10x-4 \over (x^2-2)^2}$$ |
Tworzenie pochodnej funkcji złożonej
W tablicach matematycznych jest specjalny wzór na obliczenie pochodnej funkcji złożonej, wygląda on następująco:
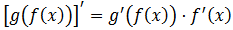
Na czym ten wzór polega? Najlepiej zaprezentowac to na przykładzie.
Przykład 6
Oblicz pochodną funkcji
$$f(x)=(3x^2+5)^3$$
Obliczenia:
Pierwszy krok to pochodna pierwszej części (mamy tutaj tylko jedną część, czyli nawias z potęgą), jest to funkcja złożona, więc według wzoru na początek liczymy pochodną całej funkcji (całego nawiasu razem z potęgą). W takim razie traktujemy to tak jakby ten nawias to było x^3, ignorujemy środek nawiasu, interesuje nas tylko zewnętrzna strona.
$$f^\prime(x)= ((3x^2+5)^3)^\prime \quad...$$
$$f^\prime(x)= 3(3x^2+5)^2 \quad...$$
Potraktowaliśmy to dosłownie tak, jakby ta funkcja wyglądała następująco:
$$f(x)=(x)^3$$
$$f^\prime(x)=3(x)^2 \quad...$$
Teraz czas na drugą część, teraz obliczamy pochodną wnętrza funkcji, czyli w tym przypadku środka nawiasu, robimy to następująco:
$$f^\prime(x)=\quad ... \quad (3x^2+5)^\prime$$
$$f^\prime(x)=\quad ... \quad 6x^2$$
Teraz tak naprawdę zignorowaliśmy potęgę i policzyliśmy tylko pochodną środka.
Na sam koniec łączymy pochodną zewnętrznej i wewnętrznej, a łączy się oczywiście mnożeniem.
$$f^\prime(x)=3(3x^2+5)^2 \times 6x^2$$
To już jest wynik, mamy obliczoną pochodną funkcji, można oczywiście wszystko przemnożyć, ale nie ma takiego wymogu w zadaniu.
Przykład 7
Oblicz pochodną funkcji
$$f(x)=\sqrt{x^3-2x^2+x}$$
Obliczenia:
W tym przykładzie postępujemy podobnie, jak przy poprzednim, ale jest pewna różnica, tym razem znajduje się tu pierwiastek, a nie nawias. Różni się to tylko funkcją zewnętrzną, co zaraz będzie można zauważyć. Zacznijmy właśnie od zewnetrznej:
$$f^\prime(x)=(\sqrt{x^3-2x^2+x})^\prime \quad ...$$
$$f^\prime(x)={1\over2\sqrt{x^3-2x^2+x}} \quad ...$$
Co tutaj się stało? ta sama zasada jak w poprzednim przykładzie, środek traktujemy jako jedną zmienną (np. x) i wyszła nam następująca funkcja:
$$f(x)=\sqrt{x}$$
$$f^\prime(x)={1\over2\sqrt{x}} \quad ...$$
Przechodzimy do drugiego kroku, wygląda on dokładnie tak samo jak w poprzednim przykładzie, obliczamy pochodną wewnętrznej.
$$f^\prime(x)=\quad ... \quad (x^3-2x^2+x)^\prime$$
$$f^\prime(x)=\quad ... \quad 3x^2-4x+1$$
Na koniec znowu łączymy zewnętrzną z wewnętrzną.
$$f^\prime(x)={1\over2\sqrt{x^3-2x^2+x}} \times (3x^2-4x+1)$$
$$f^\prime(x)={3x^2-4x+1\over2\sqrt{x^3-2x^2+x}}$$
Mamy naszą pochodną, możemy ją zostawić w takiej postaci.
Zadanie 2
Oblicz pochodną funkcji.
| a) | $$f(x)=(x+1)^2$$ | $$f^\prime(x)=2x+2$$ Wyjaśnienie: Tutaj możemy liczyć ze wzoru, ale po co, skoro mamy bardzo niskie liczby, które możemy policzyć. Na początek obliczamy potęgę zwykłej funkcji i wychodzi f(x)=x2+2x+1, właśnie teraz możemy policzyć pochodną. | |
| b) | $$f(x)=(2x^3+4x^7+57x)^{10}$$ | $$f^\prime(x)=10(2x^3+4x^7+57x)^9 \times (6x^2+28x^6+57)$$ Wyjaśnienie: Tutaj raczej nie damy rady rozwiązać tego nawiasu, dlatego trzeba użyć wzoru, mnożąc pochodną zewnętrznej i wewnętrznej, po czym wychodzi dość duży wynik. Wyniku nie trzeba szczegółowo obliczać, bo i tak zostały nam gigantyczne działania. | |
| c) | $$f(x)=\sqrt{3x^{34}-2x^{22}+10x^{12}}$$ | $$f^\prime(x)={102x^{33}-44x^{21}+120x^{11} \over 2\sqrt{3x^{34}-2x^{22}+10x^{12}}}$$ Wyjaśnienie: To zadanie może przerazić dużymi potęgami, ale nadal to jest tylko wzór, więc podstawiamy do niego obliczamy zewnętrzną, wewnętrzną, łączymy je i mamy odpowiedź. |