Matematyka

Funkcje kwadratowe

Wykres i wzory

Wykresem funkcji kwadratowej jest parabola.

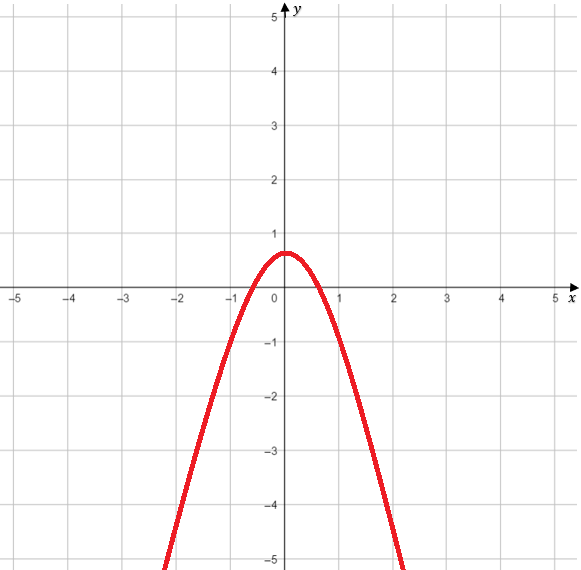
Postać ogólna funkcji kwadratowej:
f(x) = ax² + bx + c, a ≠ 0, x ∈ R

Postać kanoniczna funkcji kwadratowej:
f(x) = a(x - p)² + q, a ≠ 0, x ∈ R
W tym wzorze można odczytać współrzędne wierzchołka paraboli funkcji W(p,q)

Postać iloczynowa funkcji kwadratowej:
f(x) = a(x - x₁)(x - x₂)

Zadanie 1
Określ, czy podana funkcja jest kwadratowa

a)	$$f(x)=x^2+x^2+x+4x-43$$	To jest funkcja kwadratowa Wyjaśnienie: Po skróceniu wzoru wychodzi wzór funkcji kwadratowej (zostaje x podniesiony do kwadratu reszta nie przeszkadza).
b)	$$f(x)=x^2+51x+23+x(3-x)$$	To nie jest funkcja kwadratowa Wyjaśnienie: Po skróceniu okazuje się, że zredukował się x do kwadratu, a to oznacza, że nie jest to funkcja kwadratowa, został tylko x i stała reszta, czyli jest to funkcja liniowa (przypomnienie: we wzorze funkcji kwadratowej a nie może być równe 0).
c)	$$f(x)=x(35x+{4\over10}-50x)$$	To jest funkcja kwadratowa Wyjaśnienie: Po skróceniu pozostaje x do kwadratu i liczba stała, wystarczy nam tylko sam x do kwadratu bez wyższych potęg (i bez krojenia dziedziny), aby była to funkcja kwadratowa, a zatem jest to funkcja kwadratowa

Monotoniczność funkcji

Liczbę a nazywa się współczynnikiem kierunkowym funkcji, ponieważ to ona decyduje o tym, czy funkcja kwadratowa będzie rosła, czy malała od punktu środkowego (czy ramiona będą szły w górę, czy w dół). Każda funkcja kwadratowa ma swój środek, z którego albo maleje albo rośnie w obie strony (w stronę ujemną i dodatnią zmienia się tak samo). Współczynnik kierunkowy (a) określa więc jak będzie wyglądała parabola, czy będzie to uśmiech w dół, czy w górę.

$$ \begin{matrix} \text{Dla }a > 0 \text{ - uśmiech w górę}\\ \text{Dla }a < 0 \text{ - uśmiech w dół} \end{matrix} $$

Zadanie 2
Określ, w którą stronę będą skierowane ramiona funkcji kwadratowej.

a)	$$f(x)=25x^2+99x+25$$	Ramiona tej funkcji będą skierowane w górę Wyjaśnienie: Podano wzór ogólny, w którym można zauważyć, że współczynnik kierunkowy (a) jest równy -25, czyli jest ujemny, a zatem ramiona funkcji będą skierowane w górę.
b)	$$f(a)=ax^2+ax-a^2$$	Ramiona tej funkcji będą skierowane w dół Wyjaśnienie: Wzór tej funkcji wygląda bardzo podobnie do postaci ogólnej funkcji kwadratowej, lecz należy zauważyć, że to nie jest funkcja f(x), tylko f(a). Oznacza to, że argumentem funkcji jest a, które jest podniesione do kwadratu na samym końcu równania i jest ujemne, a więc wykresem tej funkcji będzie parabola skierowana ramionami w dół
c)	$$f(x)=5x^2+13-2x(3x-5)$$	Ramiona tej funkcji będą skierowane w dół Wyjaśnienie: W tym zadaniu należy skrócić postać, dzięki czemu można zauważyć że x podniesione do kwadratu jest ujemne, a zatem ramiona funkcji będą skierowane w dół.

Funkcja przechodząca przez punkt

Aby sprawdzić, czy funkcja kwadratowa przechodzi przez podany punkt P(x,y) wykonujemy te same czynności, jak przy innych funkcjach, czyli podstawiamy współrzędną x punktu P pod argument funkcji (dla f(x) argumentem jest x) i współrzędną y punktu P pod wartość funkcji (dla f(x) wartością jest f(x))

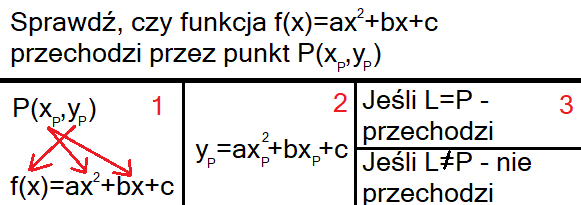
Zadanie 3
Określ, czy funkcja f przechodzi przez punkt P.

a)	$$f(x)=3x^2+5x+13 \qquad P(5,113)$$	Funkcja f przechodzi przez punkt P Wyjaśnienie: Najzwyczajniej podstawiamy dane i wychodzi 113=113 (tożsamość), więc funkcja przechodzi przez punkt P(5,113).
b)	$$f(x)=-25(x+32)^2+21 \qquad P(-31,21)$$	Funkcja f nie przechodzi przez punkt P Wyjaśnienie: Bo podstawieniu i policzeniu wychodzi nam równanie 21=-4, jest to sprzeczność, więc funkcja f nie przechodzi przez punkt P.
c)	$$f(x)=-{5\sqrt{3}\over3}(x-19\sqrt{2})^2+7 \qquad P(29\sqrt{5},\sqrt{121})$$	Funkcja f nie przechodzi przez punkt P Wyjaśnienie: Na pierwszy rzut oka może się wydawać, że będzie dużo liczenia, ale nie trzeba nawet podstawiać danych pod x, ponieważ nie ważne co podstawimy za x i tak nawias będzie dodatni (każda liczba do kwadratu jest dodatnia), a nawias jest mnożony przez ułamek ujemny, czyli cały nawias będzie ujemny. Na końcu dodajemy 7, czyli najwyżej funkcja może osiągnąć wartość 7 (y_max=7), a punkt, który badamy ma wartość y=11 (pierwiastek kwadratowy z 121 to 11), a to oznacza, że nie ważne co podstawimy pod x, to nie będzie możliwe, aby funkcja przechodziła przez punkt P. Oczywiście można także to dokładnie obliczać, ale to może zająć więcej czasu.

Obliczanie miejsc zerowych

Miejsca zerowe to nic innego jak punkt P(x,0), czyli szukamy, dla jakiego x funkcja będzie wynosiła 0. Aby obliczyć miejsce zerowe, należy w przykładowym wzorze y = ax² + bx + c podstawić 0 pod y dzięki czemu wychodzi 0 = ax² + bx + c, a tutaj mamy tylko jedną zmienną (x), więc obliczamy ją.
Aby obliczyć miejsce zerowe funkcji kwadratowej musimy mieć po jednej stronie 0. Naszym zadaniem jest sprawdzić dla jakiego x równanie będzie tożsamością, czyli kiedy druga strona będzie zerem. Jest wiele sposobów, aby to sprawdzić, dla postaci ogólnej można obliczyć deltę, której wzór jest następujący:

$$\Delta=b^2-4ac$$

Po obliczeniu dowiemy się ile funkcja ma miejsc zerowych:

$$ \begin{matrix} \text{Jeżeli }\Delta<0\text{ - brak miejsc zerowych} \\ \text{Jeżeli }\Delta=0\text{ - jest jedno miejsce zerowe} \\ \text{Jeżeli }\Delta>0\text{ - są dwa miejsca zerowe} \end{matrix} $$

Jeśli wychodzi nam brak miejsc zerowych nic więcej nie musimy już robić - po prostu nie ma miejsc zerowych, lecz jeżeli wychodzą dwa miejsca zerowe podstawiamy dane do wzoru:

$$x_1={-b-\sqrt{\Delta}\over2a}$$ $$x_2={-b+\sqrt{\Delta}\over2a}$$

Dzięki temu możemy obliczyć miejsca zerowe. W przypadku, gdy delta jest równa zero jest tylko jedno miejsce zerowe, ponieważ nie ma znaczenia czy wybierzemy pierwszy czy drugi wzór z powyższych, tak czy inaczej na górze ułamka będzie -b, więc w takim przypadku obliczamy miejsce zerowe ze skróconego wzoru:

$$x_0={-b\over2a}$$

Zadanie 4
Oblicz miejsca zerowe funkcji.

a)	$$f(x)=2x^2+3x-2$$	Funkcja f ma miejsca zerowe dla x=-2 i x=1/2 W tym zadaniu musimy standardowo obliczyć miejsca zerowe deltą. Delta jest równa 25, jest dodatnia więc będą dwa miejsca zerowe, podstawiamy do obu wzorów i obliczamy miejsca zerowe.
b)	$$f(x)=-23\sqrt[3]{27}(x+7)(x-13)$$	Funkcja f ma miejsca zerowe dla x=-7 i x=13 Wyjaśnienie: Tutaj została zaprezentowana postać iloczynowa, gdzie należy zauważyć, że gdy jakakolwiek część tej postaci będzie równa 0, całe równanie będzie równe 0, a więc możemy zbadać wszystkie części w których znajdują się zmienne (w tym przypadku x). Aby wyzerować pierwszą część (x+7) nasza zmienna musi być równa -7, bo -7+7=0. Aby wyzerować drugą część (x-13) zmienna musi być równa 13, bo 13-13=0 i tak właśnie otrzymujemy nasze miejsca zerowe.
c)	$$f(x)={23\sqrt{17}x^2+10\sqrt{10}x+9\sqrt{17}\over7\sqrt{52}+7\sqrt{121}-10\sqrt{144}}$$	Funkcja nie ma miejsc zerowych Wyjaśnienie: Te zadanie może zmylić całym ułamkiem, lecz trzeba pamiętać, że nie ważne co będzie na dole ułamka, ale jeśli na górze będzie 0, to cały ułamek będzie równy 0 (nie ważne przez co podzielimy 0 i tak zawsze będzie 0), z tego właśnie powodu nie zwracamy uwagi na dół ułamka i obliczamy deltę z górnej części (jest to postać ogólna). Licząc deltę już zauważamy, że jest ona równa -2519, a skoro jest ujemna, to znaczy, że nie ma miejsc zerowych i to właśnie jest koniec tego zadania.

Punkt wspólny kilku funkcji

Umieszczając dwie funkcje kwadratowe na wykresie (dwie parabole), mogą one mieć jeden punkt wspólny, dwa punkty wspólne, nieskończenie wiele punktów wspólnych lub mogą nie mieć ich wcale.

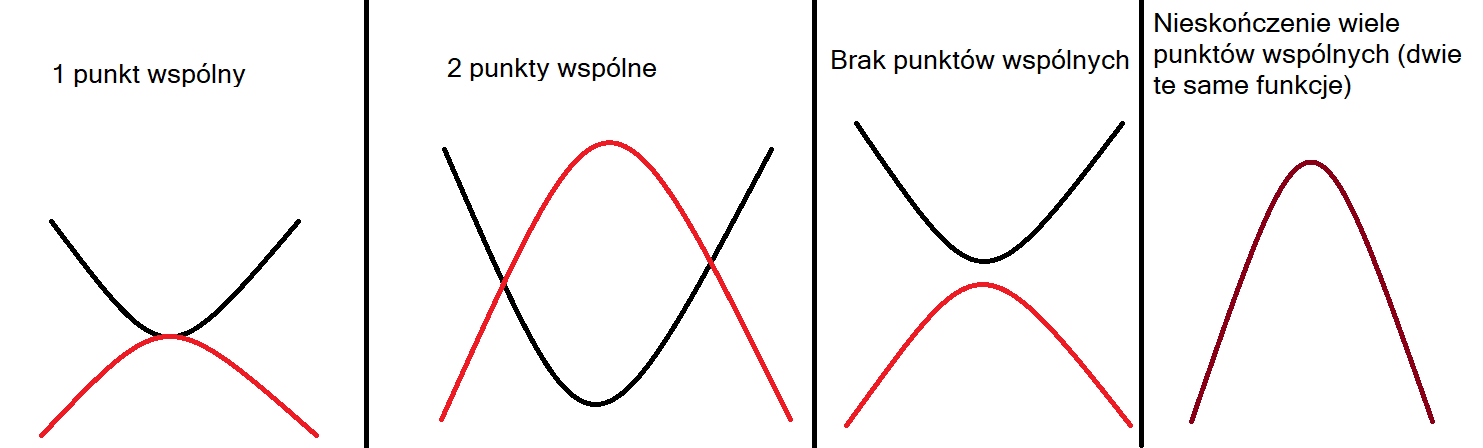
Sprawdzając, ile punktów wspólnych mają dwie funkcje, należy obie zamknąć w jednym układzie równań i rozwiązać go odpowiednią metodą.

Przykład
Sprawdź, ile punktów wspólnych mają dwie podane funkcje
y=ax² + bx + c
y=kx² + lx + m
Rozwiązanie:

$$ \begin{cases} y=ax^2 + bx + c \\ y=kx^2 + lx + m \end{cases}$$

Jeżeli wyszła tożsamość (np.: 10=10, 0=0), to funkcje pokrywają się, więc mają nieskończenie wiele punktów wspólnych. W przypadku sprzeczności (np.: 0=5, 10=3) są to funkcje rozłączne, czyli nie mają punktów wspólnych. Jeśli wychodzi konkretny wynik (np.: y=4 i x=1), to w zależności od ilości wyników (mogą być dwa różne wyniki lub tylko jeden wynik) tyle rozwiązań ma dana funkcja. Aby określić, gdzie znajduje się pojedynczy punkt wspólny, należy obliczyć z układu x=? i y=? i podstawić do danych punktu P(x,y) (w przypadku dwóch rozwiązań robimy to samo, tylko osobno dla każdego punktu wspólnego).

Zadanie 5
Określ, ile punktów wspólnych mają podane proste, w przypadku pojedynczego punktu wspólnego lub dwóch punktów wspólnych oblicz ich współrzędne.

a)	$$2y=6x^2-3$$$$y=3x^2-5x+1$$	Funkcje mają jeden punkt wspólny P(1/2,-3/4) Wyjaśnienie: Po zamknięciu wzorów funkcji w układzie równań skorzystałem z metody przeciwnych współczynników (pomnożyłem dolną funkcję przez (-2)). Ostatecznie wyszedł wynik x=1/2, więc podstawiłem go pod pierwsze lepsze równanie z układu i wyszło y=-3/4, na samym końcu wystarczy podstawić dane pod współrzędne punktu i wyszedł punkt wspólny P(1/2,-3/4)
b)	$$y=2x^2+3x-5$$$$y=-x^2+2x+5$$	Funkcje mają dwa punkty wspólne P₁(-2,-3) i P₂(5/3,50) Wyjaśnienie: Po zamknięciu tych funkcji w układzie równań użyłem metody przeciwnych współczynników i wyszło równanie kwadratowe (0=3x² + x - 10). Takie równanie można rozwiązać metodą, jaką używaliśmy przy miejscach zerowych, czyli delta. Po obliczeniu wyszły mi dwa wyniki, dlatego funkcje będą miały dwa punkty wspólne. Otrzymane wyniki to współrzędne x dwóch punktów, aby obliczyć współrzędne y należy podstawić każdy x pod obojętnie jakie równanie w układzie i wyjdzie odpowiedź, na końcu trzeba podstawić dwa zestawy pod współrzędne punktów i wychodzi wynik.
c)	$$y=-\sqrt{72}(x+13\sqrt{32})^2+21$$$$y=\sqrt{104}(x-7\sqrt{8})^2+22$$	Funkcje nie mają punktów wspólnych Wyjaśnienie: Na początku te zadanie może wydawać się trudne, ale takie nie jest. Możemy zauważyć, że obie funkcje zostały zapisane w postaci kanonicznej, co oznacza, że mamy współrzędne wierzchołków. Wiemy także, w którą stronę są skierowane ramiona funkcji, a zatem przeanalizujmy to: Wierzchołek pierwszej funkcji jest na wysokości y=21 i jej ramiona są skierowane w dół (przed nawiasem jest minus, czyli a=-1), natomiast wierzchołek drugiej funkcji znajduje się wyżej od poprzedniej - na wysokości y=22, ramiona tej funkcji są skierowane w górę (nie ma minusa przed nawiasem). Zauważając to można wywnioskować, że jeżeli funkcja pierwsza jest wyżej od drugiej i idzie tylko w górę, a druga tylko w dół, to nigdy się nie spotkają, to oznacza też, że nie będą miały punktów wspólnych.