Funkcje liniowe
Wykres i wzór ogólny
Wykresem funkcji liniowej jest prosta
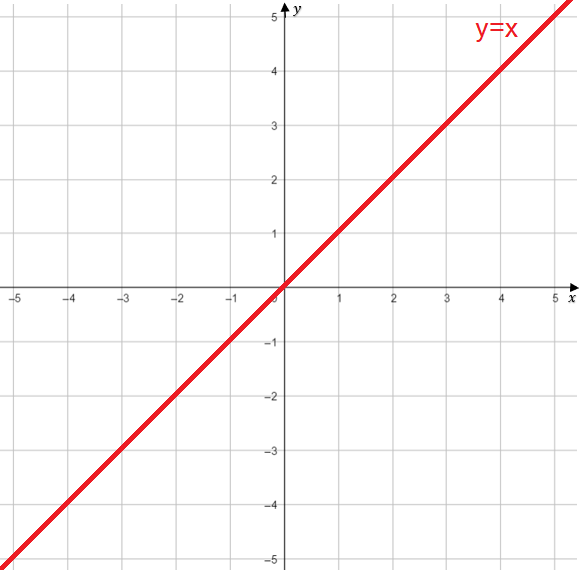
f(x) = ax + b, x ∈ R
Zadanie 1
Określ, czy podana funkcja jest liniowa
| a) | $$f(x)=\sqrt{507 \times 32\over {32^2}}\times x$$ | To jest funkcja liniowa Wyjaśnienie: Nie ważne co dzieje się ze stałymi liczbami, aby określić, czy funkcja jest liniowa należy spojżeć na zmienną, w tym przypadku jest to x, która jest bez żadnej potęgi. Cały pierwiastek możemy potraktować jako stałą a i wtedy wychodzi nam wzór f(x)=ax, czyli wzór funkcji liniowej (b w tym przypadku jest równe 0) | |
| b) | $$f(b)=x+b^2$$ | To nie jest funkcja liniowa Wyjaśnienie: Tutaj trzeba zauważyć, że zmienną nie jest x, lecz b (ponieważ f(b)), dlatego właśnie x jest liczbą stałą, co oznacza, że kwadrat z x nadal jest liczbą stałą. Aby sprawdzić jaka to funkcja musimy przyjżeć się zmiennej b, która jest podniesiona do drugiej potęgi, dlatego właśnie nie jest to funkcja liniowa (jest to funkcja kwadratowa) | |
| c) | $$f(a)=10$$ | To jest funkcja liniowa Wyjaśnienie: Tym razem przyrównując to do wzoru wychodzi że a=0, i b=10 (oczywiście przyjmując że zmienna a to x), lecz w teorii można tak samo podstawić wzór funkcji kwadratowej, gdzie a=0, b=0 i c=10, wtedy także wyszło by f(x)=10, dlatego właśnie należy przyjżeć się wykresowi, który będzie stale wynosił 10, czyli będzie linią prostą poziomą |
Monotoniczność funkcji
Liczbę a nazywa się współczynnikiem kierunkowym funkcji, ponieważ to ona decyduje o tym, czy funkcja liniowa będzie rosła, czy malała lub może będzie stała.
Zadanie 2
Określ, czy funkcja jest malejąca, stała lub rosnąca.
| a) | $$f(x)={37x\over500^2}$$ | Funkcja rosnąca Wyjaśnienie: Nie ważne przez jak gigantyczną liczbę dodatnią podzielimy drugą liczbę dodatnią, będzie ona nadal dodatnia, dlatego właśnie a > 0, więc funkcja jest rosnąca. | |
| b) | $$f(d)=-d*{({1\over2}-{1\over3})\over(-{1\over2})^2}+\sqrt[3]{125}-{4\over2}$$ | Funkcja malejąca Wyjaśnienie: Całkowicie ignorujemy część po plusie, ponieważ to jest nasze b, my potrzebujemy tylko współczynnika kierunkowego, czyli a. Po przeliczeniu pierwszej części wychodzi, że a= -2/3, czyli a jest mniejsze od zera, a to oznacza, że funkcja jest malejąca | |
| c) | $$f(a)=((19+53)^2-(34+38)^2) \times a \times {{2^{10}\over1024}-\pi^2\times3,94\over\sqrt{81}\times\pi} + 46725386892347\pi$$ | Funkcja stała Wyjaśnienie: Ignorujemy część po ostatnim plusie, obliczamy tylko współczynnik kierunkowy. Już na początku widać, że po dodaniu liczb w obu nawiasach podniesionych do kwadratu wychodzą te same liczby (72), więc nie trzeba tego podnosić do potęgi, ponieważ tak czy inaczej wyjdzie 0, a jak wiadomo zero mnożąc przez cokolwiek zawsze wyjdzie zero, a to oznacza, że a=0, czyli funkcja jest stała. |
Funkcja przechodząca przez punkt
Aby sprawdzić, czy funkcja przechodzi przez dany punkt P(x,y) wystarczy podstawić we wzorze funkcji f(x)=ax+b pod x współrzędną x punktu P i pod f(x) współrzędną y punktu P, jeśli to równanie będzie tożsame, to oznacza, że funkcja przechodzi przez punkt P, jeśli będzie sprzeczne, to funkcja nie przechodzi przez punkt P
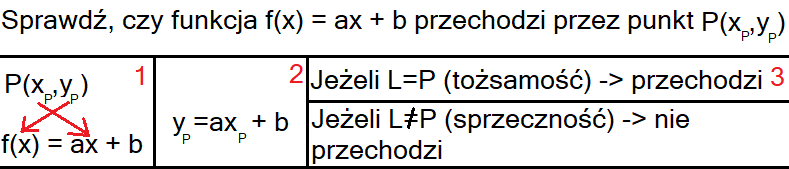
Zadanie 3
Określ, czy funkcja f przechodzi przez punkt P.
| a) | $$f(x)={2\over3}x+7\qquad P(6,11)$$ | Funkcja przechodzi przez punkt P Wyjaśnienie: We wzorze funkcji f(x) podstawiamy liczbę 6 za x i liczbę 11 za f(x), ostatecznie wychodzi 11=11, czyli równanie się zgadza, co oznacza, że funkcja przechodzi przez punkt P(6,11) | |
| b) | $$f(x)=-x+4 \qquad P(-2,5)$$ | Funkcja nie przechodzi przez punkt P Wyjaśnienie: Znowu podstawiamy odpowiednio współrzędną x punktu P do argumentu (x) funkcji i współrzędną y punktu P do wartości (f(x)) funkcji. Po przeliczeniu wychodzi równanie 5=6, czyli sprzeczność, a to oznacza, że funkcja f(x) nie przechodzi przez punkt P(-2,5) | |
| c) | $$f(x)=35\sqrt{2}x-(6^2+6-\sqrt{3}) - 14\sqrt{2}x \qquad P(\sqrt{2},\sqrt{3})$$ | Funkcja przechodzi przez punkt P Wyjaśnienie: Ponownie podstawiamy współrzędne do odpowiednich składowych funkcji. Wychodzi równanie:$$\sqrt{3}=\sqrt{3} \qquad L=P$$Jest to tożsamość, czyli funkcja f przechodzi przez punkt P |
Punkt wspólny kilku funkcji
Umieszczając dwie funkcje liniowe na wykresie (dwie proste), mogą one mieć jeden punkt wspólny (przecinające się), nieskończenie wiele (pokrywające się) lub mogą nie mieć ich wcale (rozłączne).

Sprawdzając, ile punktów wspólnych mają dwie funkcje, należy obie zamknąć w jednym układzie równań i rozwiązać go odpowiednią metodą.
Przykład
Sprawdź, ile punktów wspólnych mają dwie podane funkcje
y=ax + b
y=cx + d
Rozwiązanie:
Jeżeli wyszła tożsamość (np.: 10=10, 0=0), to funkcje pokrywają się, więc mają nieskończenie wiele punktów wspólnych. W przypadku sprzeczności (np.: 0=5, 10=3) są to funkcje rozłączne, czyli nie mają punktów wspólnych. Jeśli wychodzi konkretny wynik (np.: y=4 i x=1), to znaczy, że funkcje mają jeden punkt wspólny. Aby określić, gdzie znajduje się pojedynczy punkt wspólny, należy obliczyć z układu x=? i y=? i podstawić do danych punktu P(x,y)
Zadanie 4
Określ, ile punktów wspólnych mają podane proste, w przypadku pojedynczego punktu wspólnego oblicz jego współrzędne.
| a) | $$3y=5x+6$$$$3y=11x+30$$ | Proste mają jeden punkt wspólny P(-4,-14/3) Wyjaśnienie: Należy oba równania zamknąć we wspólny układ równań, użyłem sposoby przeciwnych współczynników, czyli pomnożyłem górne równanie przez -1 i dodałem wszystkie równania w układzie, poskutkowało to tym, że zmienna y się skróciła, zostało tylko x w równaniu 0 = 6x + 24, wychodzi tu x=-4 (już wiemy, że proste mają jeden punkt wspólny - wyszedł konkretny x). Później podstawiamy x pod byle jakie równanie w układzie, żeby obliczyć y. Na koniec podstawiamy do współrzędnych punktu P(-4,14/3) | |
| b) | $$y=3x+10$$$$7y=21x+22$$ | Proste nie mają punktów wspólnych Wyjaśnienie: Znowu używam metody przeciwnych współczynników: pierwsze równanie mnożę przez -7 i dodaję oba równania. Ostatecznie wychodzi 0=-48, czyli sprzeczność, a zatem proste nie mają punktów wspólnych | |
| c) | $$3y=12x+9$$$$y=4x+3$$ | Proste mają nieskończoność punktów wspólnych Wyjaśnienie: Ponownie używam metody przeciwnych współczynników: tym razem mnożę przez -3 drugie równanie i sumuje oba, ostatecznie wychodzi 0=0, czyli tożsamość, co oznacza, że proste pokrywają się i mają nieskończoność punktów wspólnych |
Obliczanie miejsc zerowych
Miejsca zerowe to nic innego jak punkt P(x,0), czyli szukamy, dla jakiego x funkcja będzie wynosiła 0. Aby obliczyć miejsce zerowe, należy w przykładowym wzorze y = ax + b podstawić 0 pod y dzięki czemu wychodzi 0 = ax + b, a tutaj mamy tylko jedną zmienną (x), więc obliczamy ją i mamy odpowiedź
Zadanie 5
Oblicz miejsce zerowe funkcji.
| a) | $$y=5x+3$$ | Funkcja ma miejsce zerowe dla x=-3/5 Wyjaśnienie: Podstawiamy pod y liczbe 0 i wychodzi równanie 0=5x+3, rozwiązaniem tego równania jest nasze miejsce zerowe czyli x=-3/5 | |
| b) | $$3y=x-5$$ | Funkcja ma miejsce zerowe dla x=5 Wyjaśnienie: Znowu podstawiamy pod y liczbę 0 i wychodzi równanie 0=x-5, po przekształceniu wychodzi x=5 | |
| c) | $$y={x\over2}+{x\over3}-{25x\over30}+20$$ | Funkcja nie ma miejsc zerowych Wyjaśnienie: Ponownie podstawiamy 0 zamiast y i rozwiązujemy równanie, x całkowicie się skraca, przez co wychodzi 0=20, jest to sprzeczność, a więc funkcja nie ma miejsc zerowych |